Pool Survival Analysis

FPPS transfers profit volatility from hashers to the pool operator, but how much do pools need in reserve?

Recent findings by mononaut and 0xB10c show that bitcoin is far more centralised than previously thought. It has been speculated that the reason is that as a market, miners are increasingly demanding consistent payouts (FPPS) which shifts the volatility exposure (risk) from individual miners (hashers) to the pool, which must pay out regardless of how many blocks have been found.

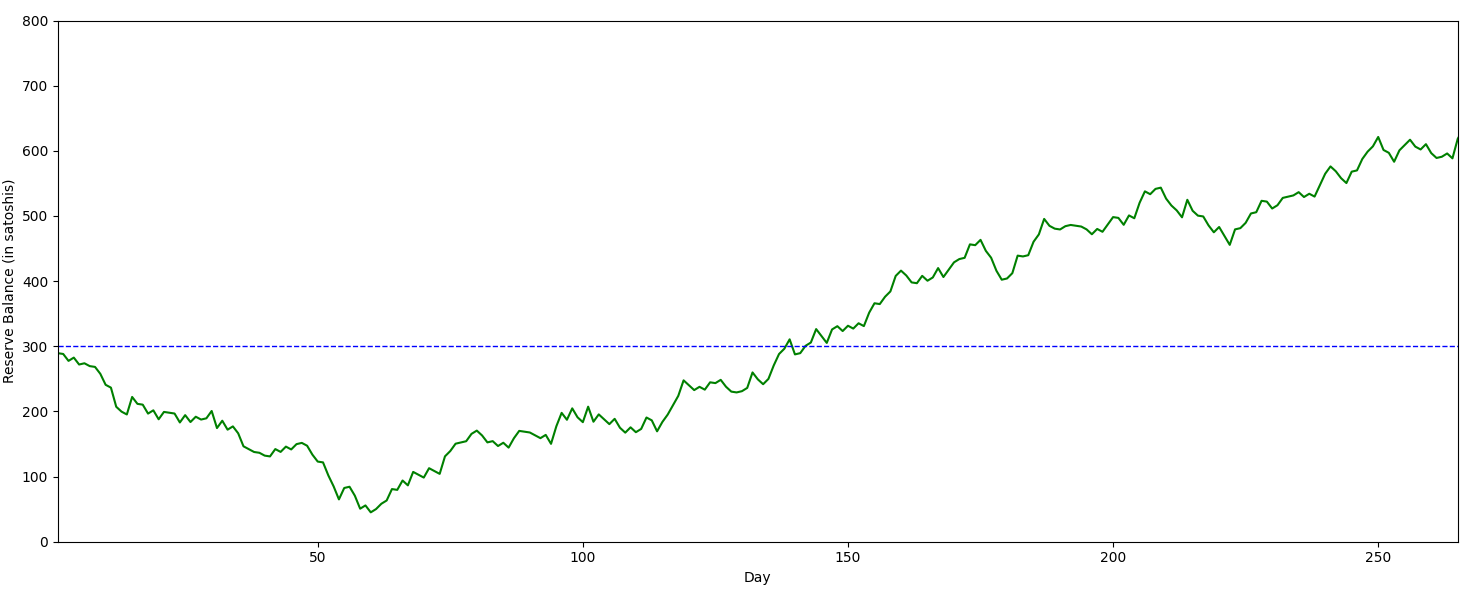
Larger pools have more consistent (less volatile) income. However, larger pools also have to pay out larger amounts than smaller pools. It was not obvious to me how pool size (% of network hashrate) correlates to the reserve funds required to obtain a particular statistical chance of survival.

Bitmex research performed interesting analysis of how much BTC is required for pools with 5 and 50% of the hashrate.

As mentioned in this work, the outstanding question is how does the 95% survivorship threshold change across a range of hashrates. This is the analysis that I have performed.

Human intervention doesn't help

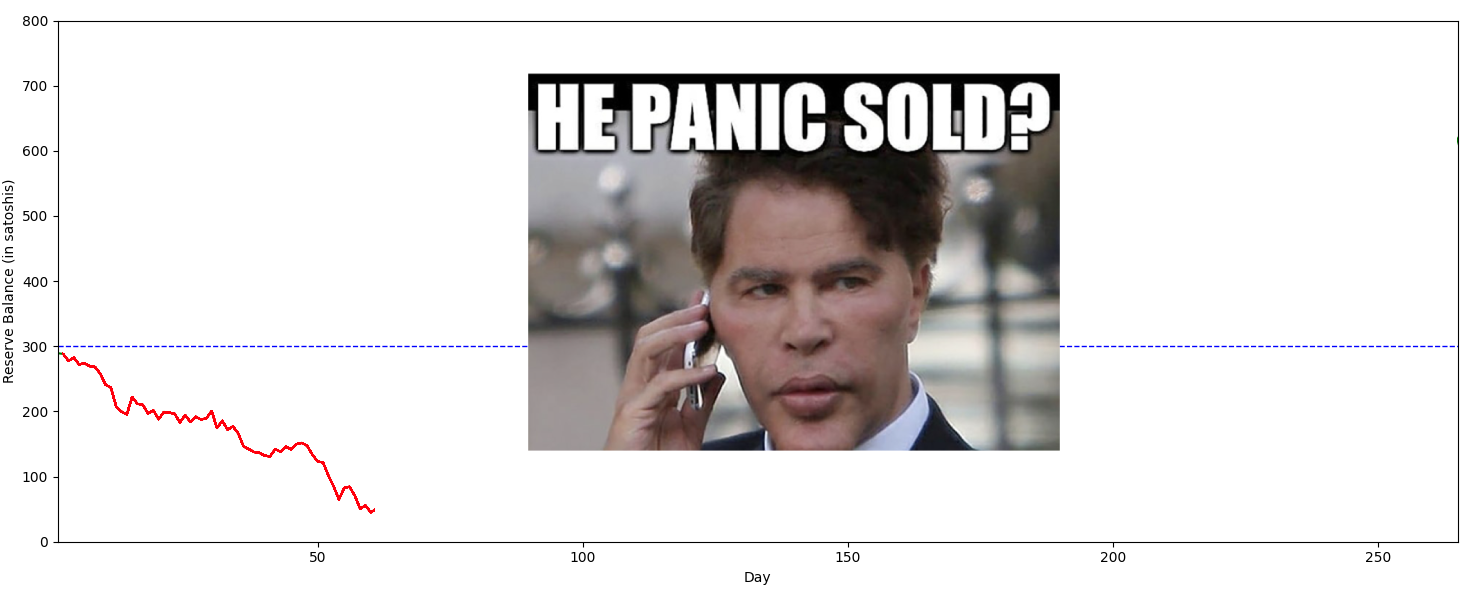
It's easy to fall for the trap of thinking that the pool would just stop before losing hundreds of bitcoin in their reserves, but in reality this just reduces the true reserve value. Imagine a pool which started with 300 BTC reserves and watched it dwindle to 50 BTC. If they stop the pool, they only really had 250 BTC. The reason they don't sell is because there is a small chance the pool could recover to over double it's initial reserves from accumulated profits.

The only difference between these two runs, is that one pool panic sold.

Model Implementation

To replicate this I implemented the model in python using the same assumptions as the bitmex research.

There are two main functions in the script, simulate_mining and find_min_reserve_binary_search

simulate_mining: Simulates daily profit/loss from a constant payout pool after a specified number of days. Thousands of runs are simulated. At the end of the simulation the percentage of runs which never dropped below zero is returned. The simulate_mining function akin to a random walk

find_min_reserve_binary_search: This function uses a binary search algorithm to find the minimum starting reserve needed for the pool to have a specified chance of survival (95% or 99%). It runs the simulate_mining function and depending on the result adjusts the estimated reserves up or down to identify the smallest reserve that still meets the target survival rate.

In the future the simulation script could be adapted to more accurately model the FPPS payout structure by incorporating the effect of volatile network fees.

Implementation Check

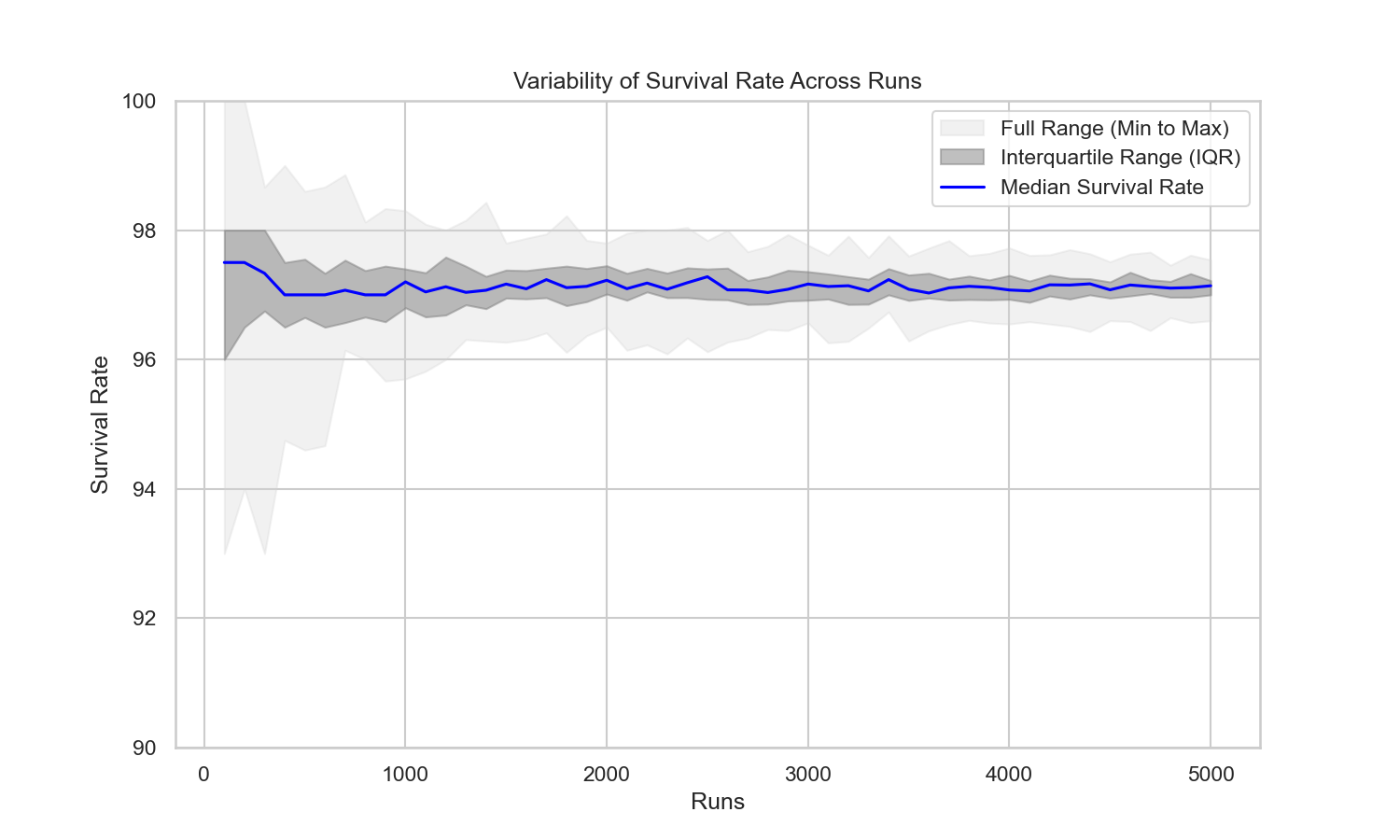
First let us check how my implementation of the model compares to the findings by bitmex. I run an analysis to see how the survival rate converges with the number of model runs for a scenario where a 5% pool has 300 BTC reserves. Bitmex research calculated a rate of 97.8%, my implementation converges on a similar value of approx 97%.

Variability in run result (50 samples) For 5%, 300 BTC, 1 year.

Next we check the survival rate for a 50% pool with 300 BTC. My model converges on 95%, matching the value reported by bitmex research of 95%.

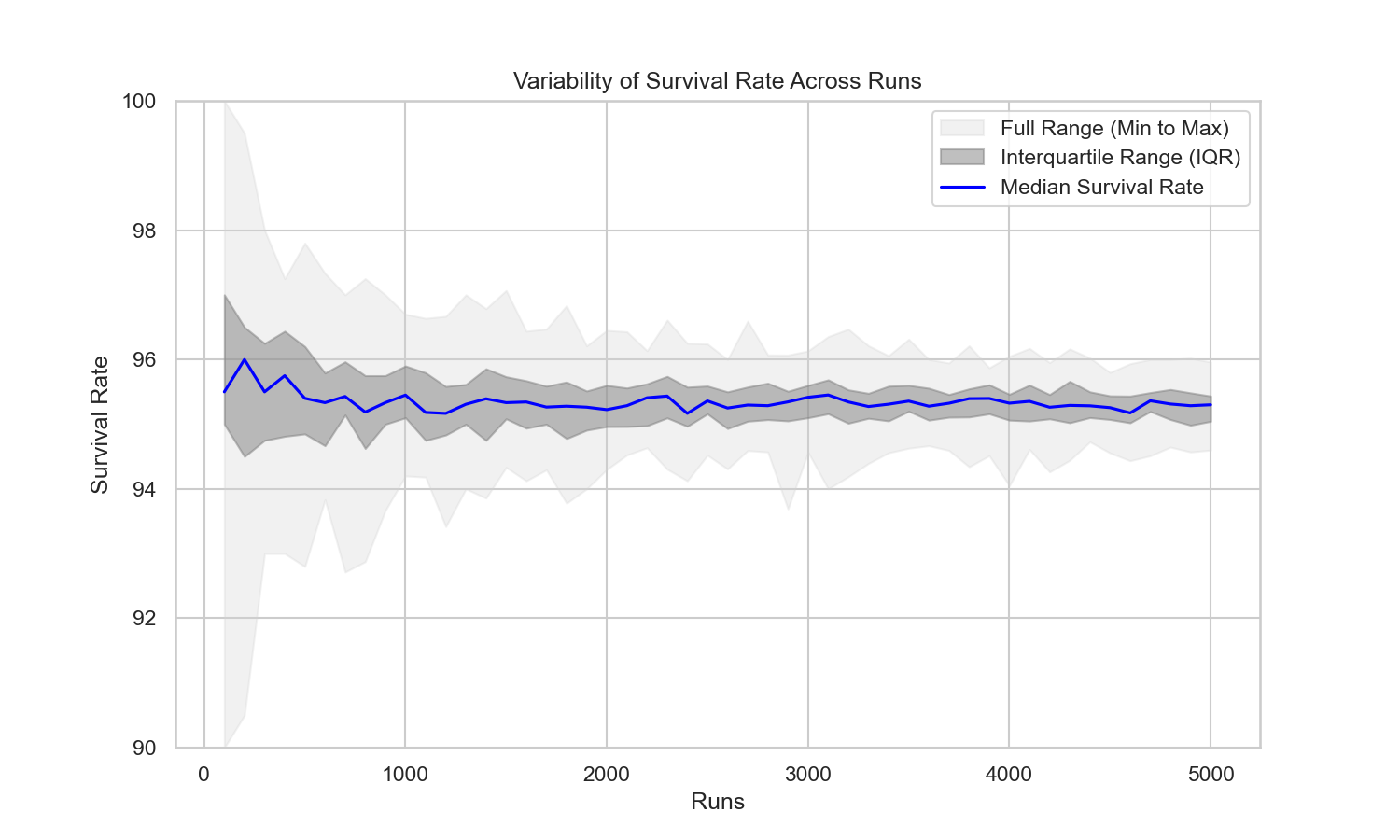
Variability in run result (50 samples) For 50%, 400 BTC, 1 year.

As we can see from these graphs, we can average the result from 50 cycles of 1000 runs and we will be close to the true value. The alternative is to increase the number of runs well beyond 5000.

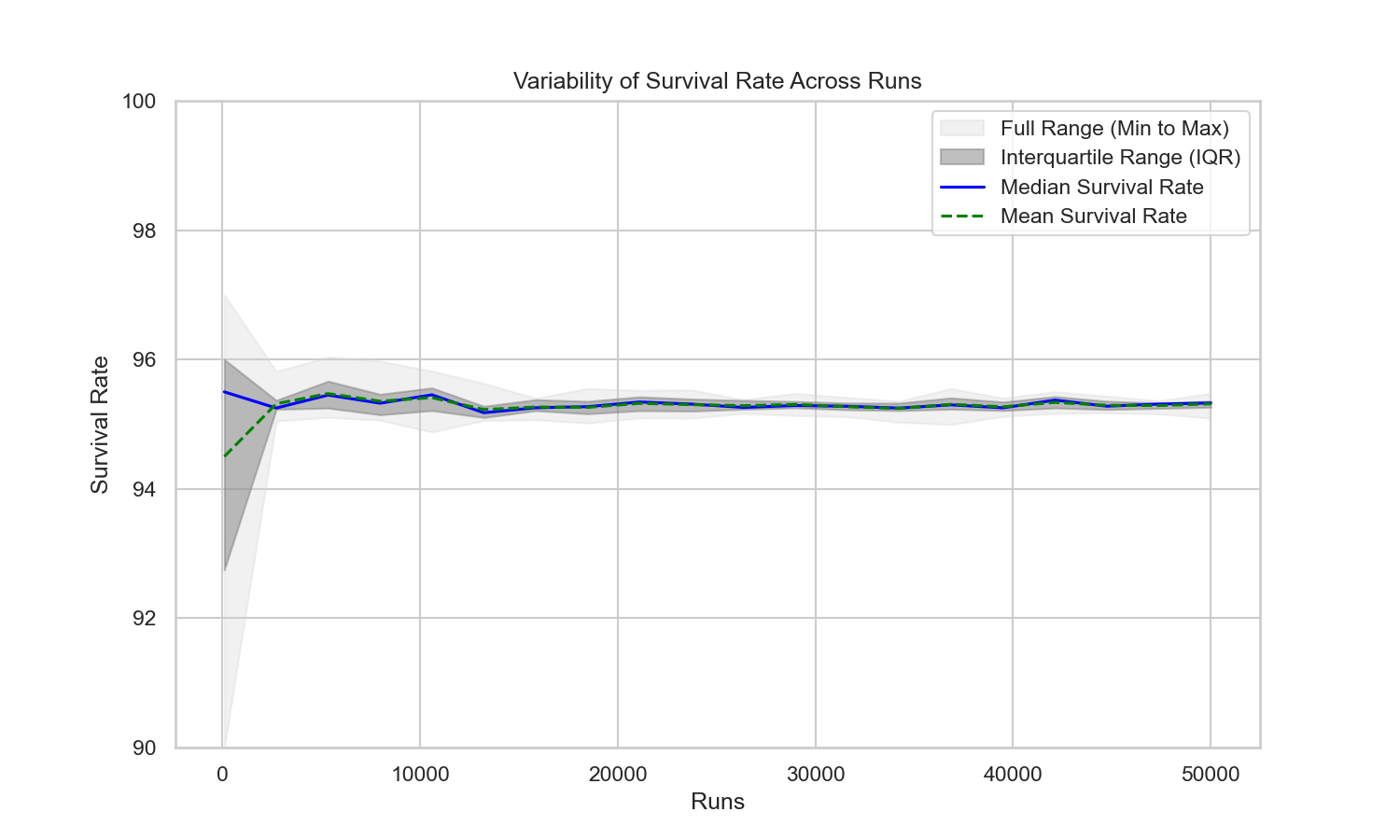
Clearly it is better to perform more runs, but there is diminishing returns in accuracy. Even with 50,000 runs there is still a range of ~0.4% so we will run with multiple cycles to reduce the variation. There are more intelligent ways to compute the correct result using statistical methods, but compute is ~free so i'll just nest everything in a for loop and let the computer do all the hard work.

Findings

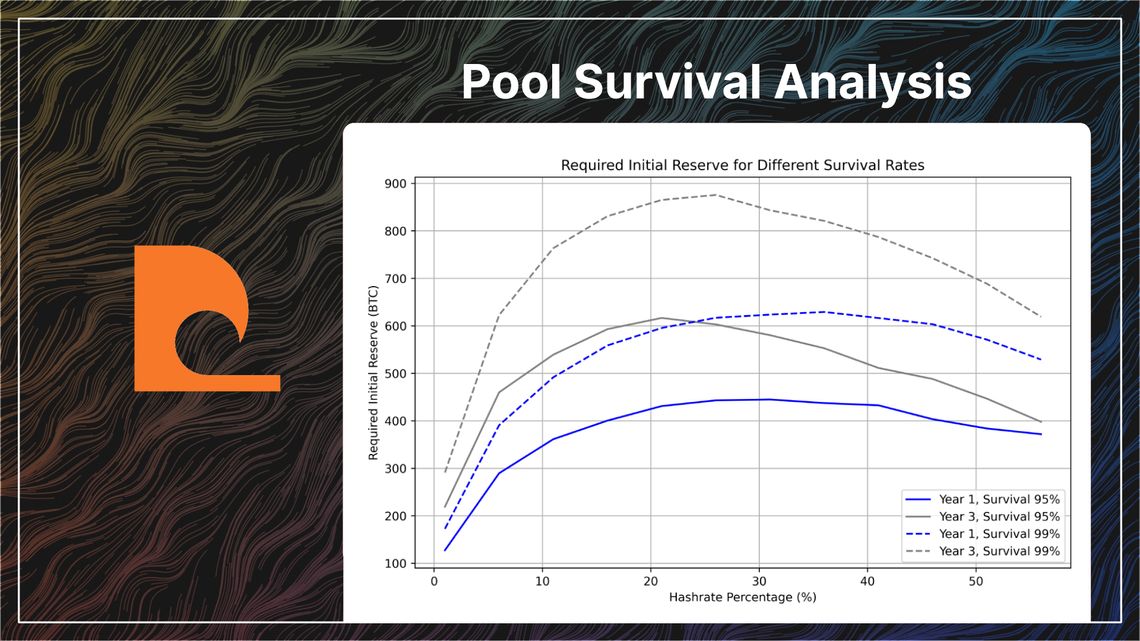
Lets plot required initial reserve to have a 95% and 99% survival rate for both 1 year and 3 years.

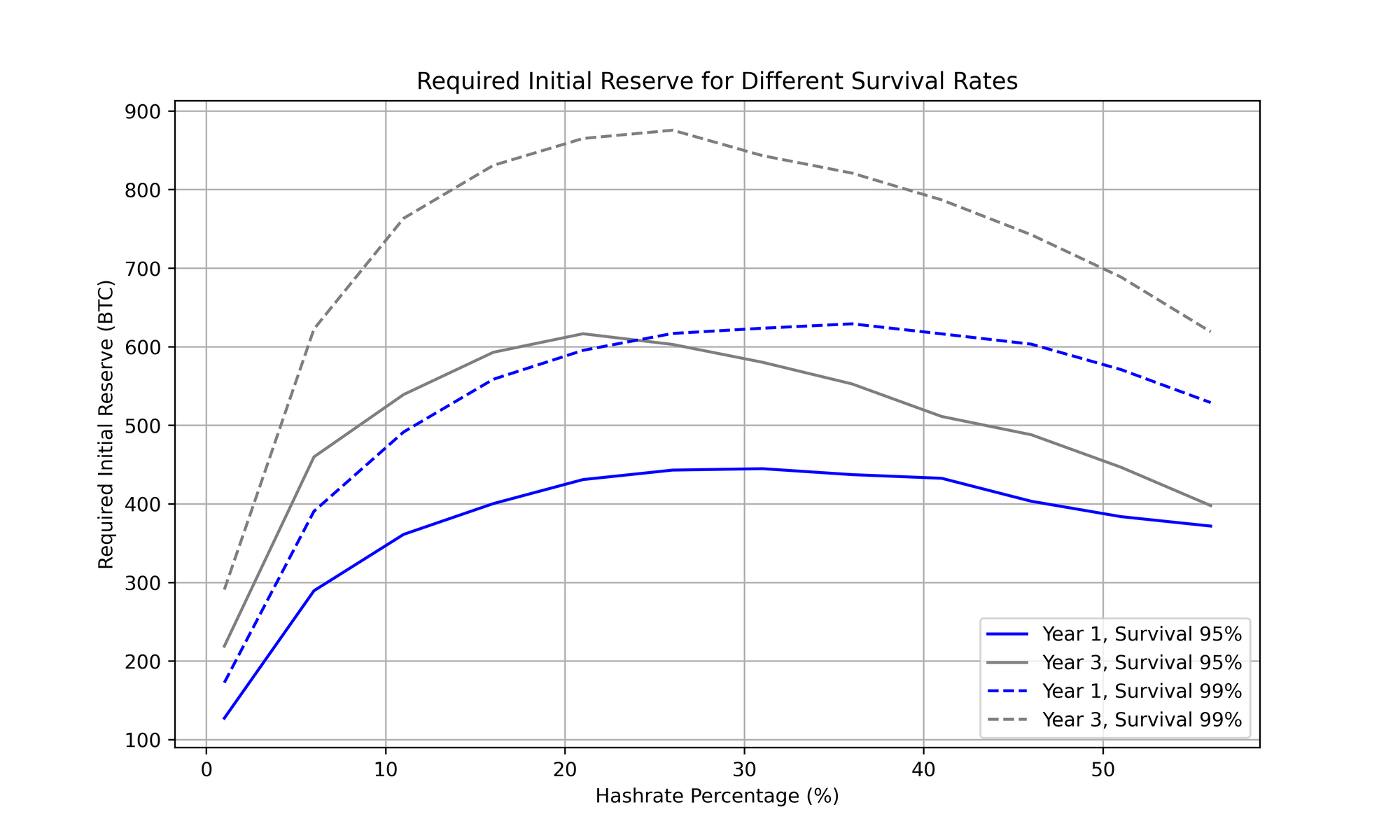
For each scenario there is a maximum required initial reserve, which corresponds to a threshold hashrate above which the required initial reserve decreases.

To have a 95% chance of survival after 1 years a pool requires no more than 450 BTC ($27M USD), with marginally diminishing cost above ~30% of hashrate.
To have a 99% chance of survival after 3 years a pool requires almost 900 BTC ($54M USD), with a significantly diminishing cost above ~25% of hashate.

This means that particularly over long (3+ year) durations, pools near these threshold hashrates need larger reserves than both smaller and larger competitors. Put differently, for a given reserve size, some large pools have a higher chance of survival than some smaller pools near the threshold.

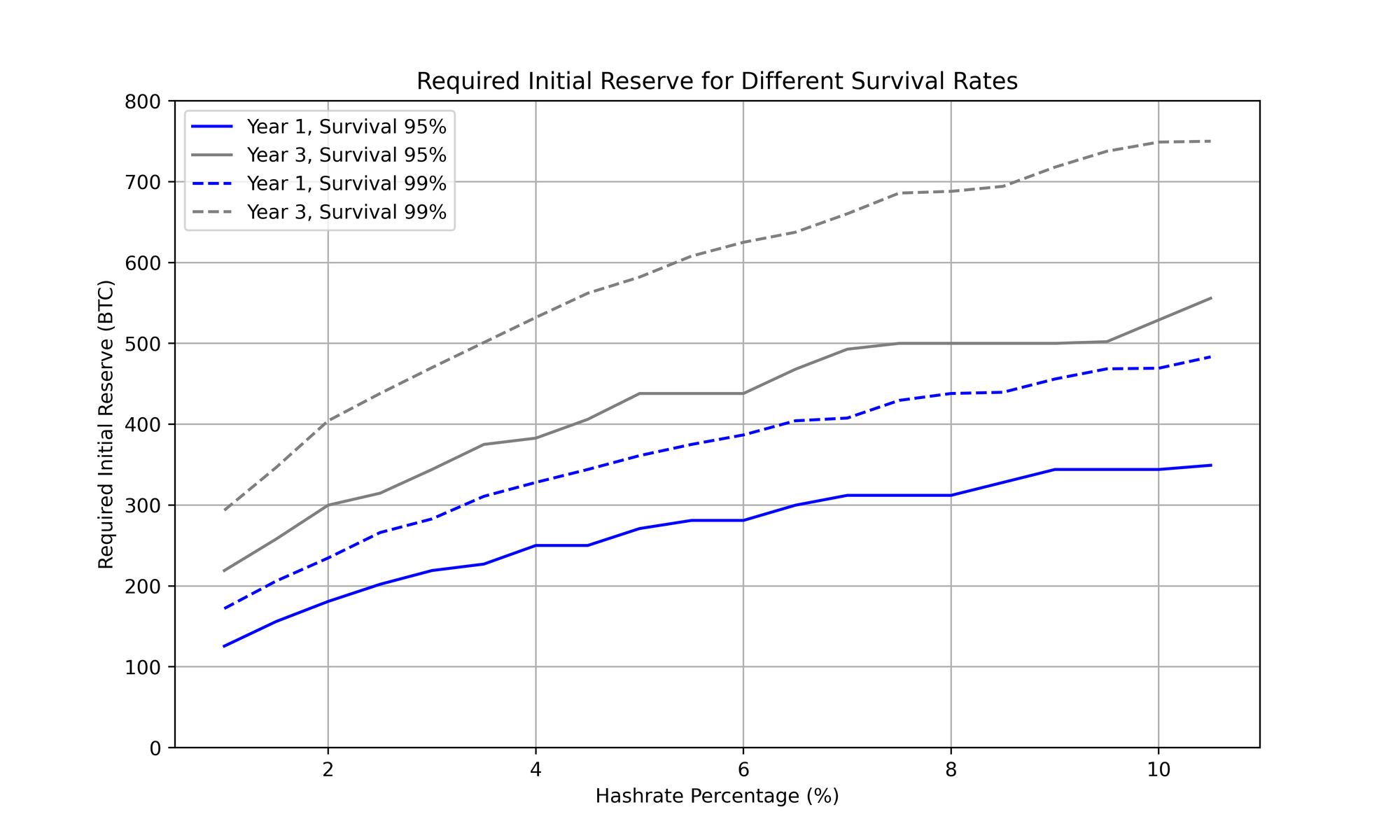
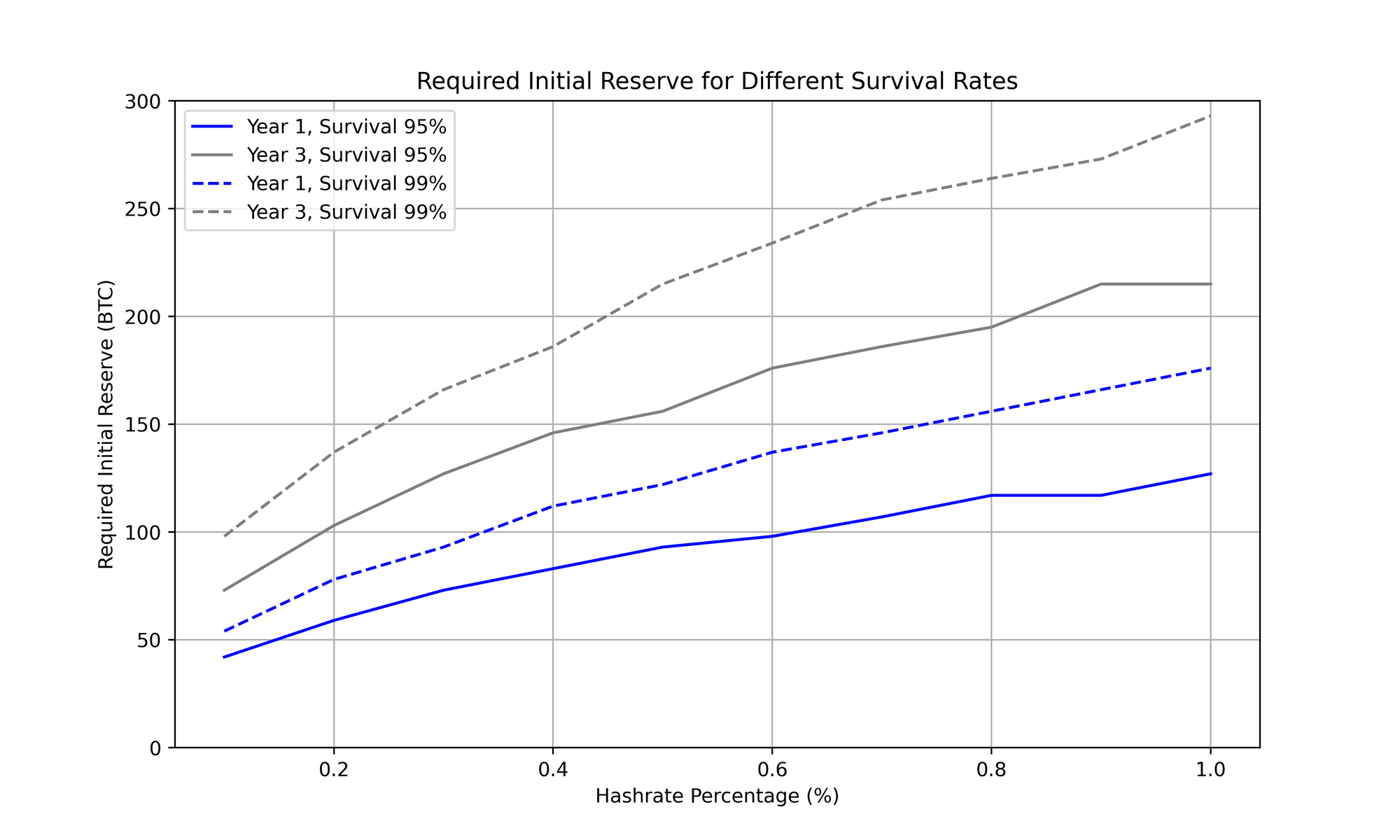
Zooming in we can see how the required reserves change below 10%.

Zooming in we can see how the required reserves change below 1%.

The observed relationship between required initial reserves and pool hashrate is of interest given the high degree of pool centralisation today, the economy of scale that comes from having significant hashrate (30%+) can be clearly seen, even ignoring the additional options available to a large malicious miner (such as orphaning blocks and driving up FPPS payments with high fee self spends).

If you have thoughts about this post and want to chat drop me a message

Human intervention doesn't help

Model Implementation

Implementation Check

Findings

More by orange surf

Dude. Where's my Block

testnet